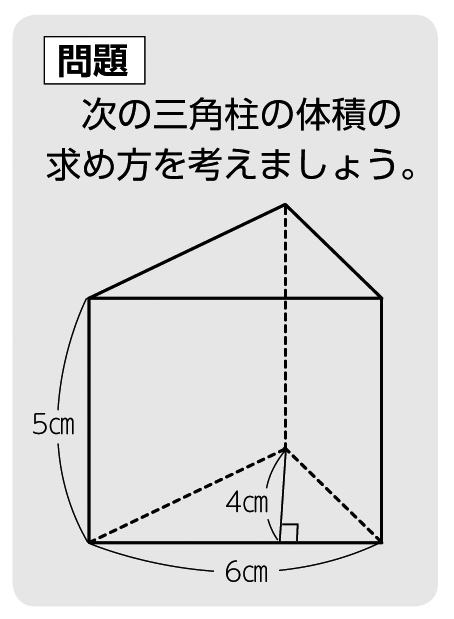
次の柱の問題を解きましょう。 円柱と三角柱の体積の公式を答えてから計算してください。 問1. 柱とはどういう特徴がある図形のことをいいますか。 問2. 円柱と三角柱の図形を描きましょう。 問3. 四角柱、六角柱とはどういう図形ですか。 問4.1 三角柱の体積を計算で求める方法を 理解する。 既習の立体の体積の求め方を手がかりに、角 柱の体積の求め方を見直す。 *底面が直角三角形の三角柱の体積も、底面積 ×高さで求められることを考える。 2 一般の角柱の体積の公式をまとめ る。三角すいの内部で、一方向へ縮んだ三角すいの体積は、以下の公式で求めることができます。 全体の体積に、 、 、 をかけたものが、小さい三角すいの体積です。 この 、 、 をかけ合わせた分数が、本講義で"ちぢみ率"と呼んでいるもの。 ちぢみ率は
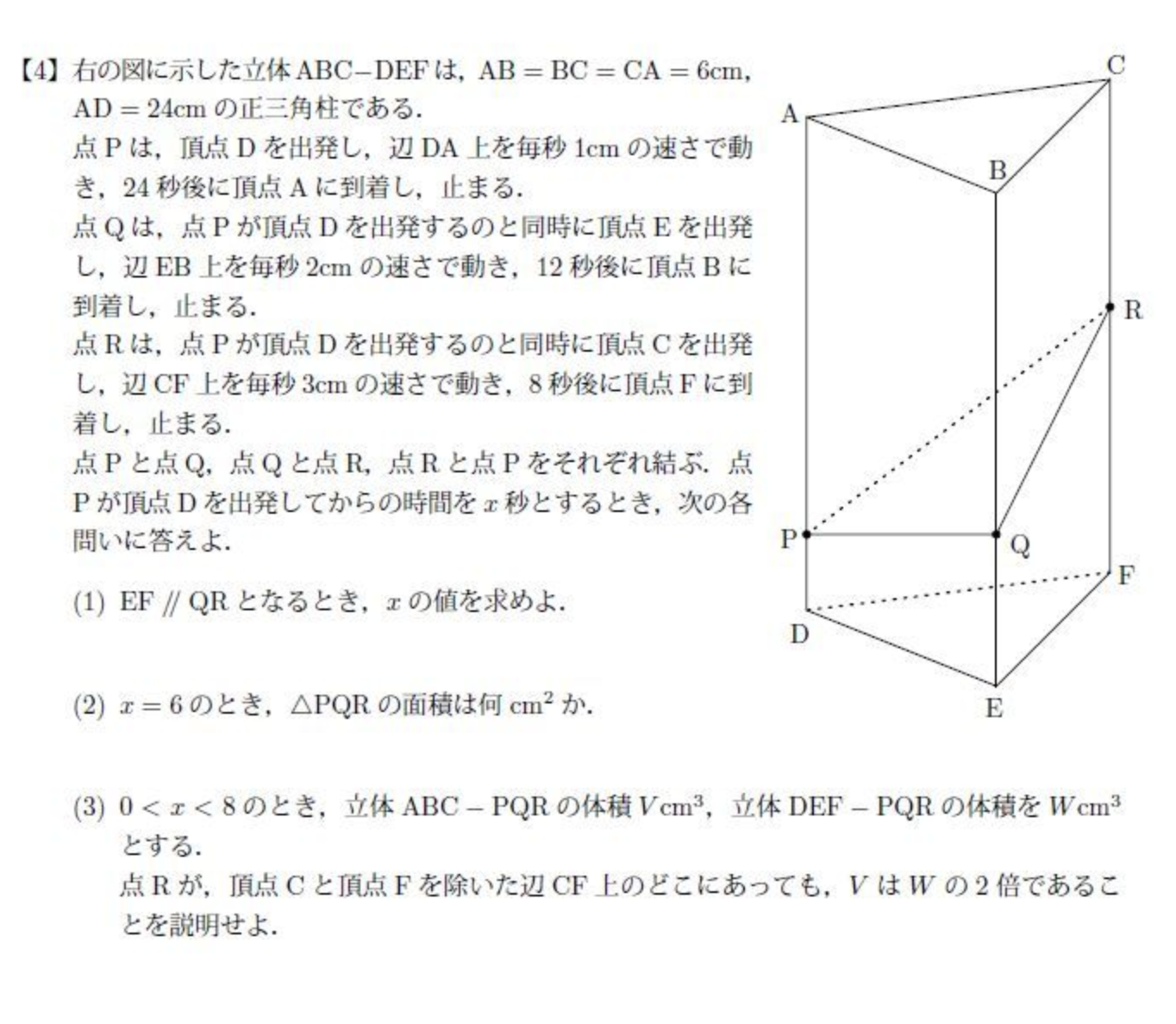
3分で分かる 三角柱の体積 表面積の公式 表面積 をわかりやすく 合格サプリ
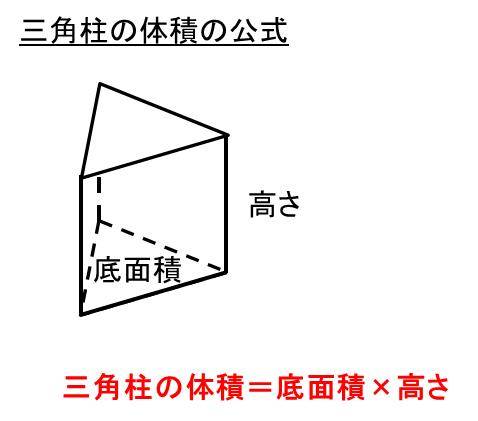
三角柱の体積の公式
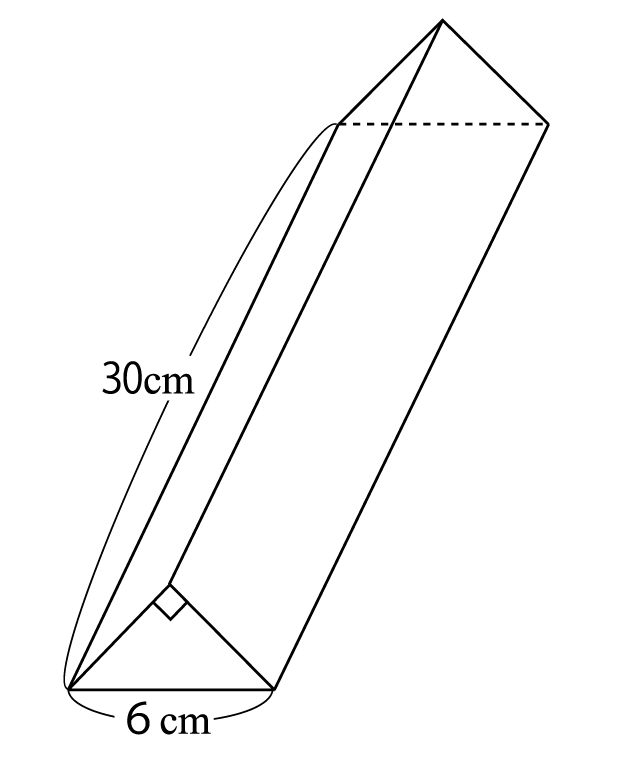
三角柱の体積の公式-柱体の体積は小学校の頃に習いましたが、復習しつつしっかり抑えていきましょう。 目次 角柱・円柱の体積(小学校算数の復習) 角柱・円柱の体積の公式 |小学生に教えるための分かりやすい解説 角柱や円柱の体積は決まった公式に当てはめるだけで求められるので、問題を解くのはそ� · 上の三角柱の体積の公式を元に計算していきます。 4×3÷2×5=30cm3(立方センチメートル) と求めることができるのです。 まとめ 三角柱の表面積(底面積も)と体積を求める公式と計算問題単位との関係




体積の求め方 計算公式一覧
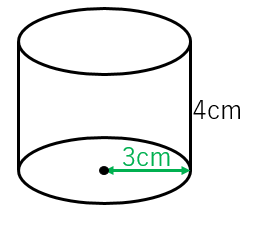
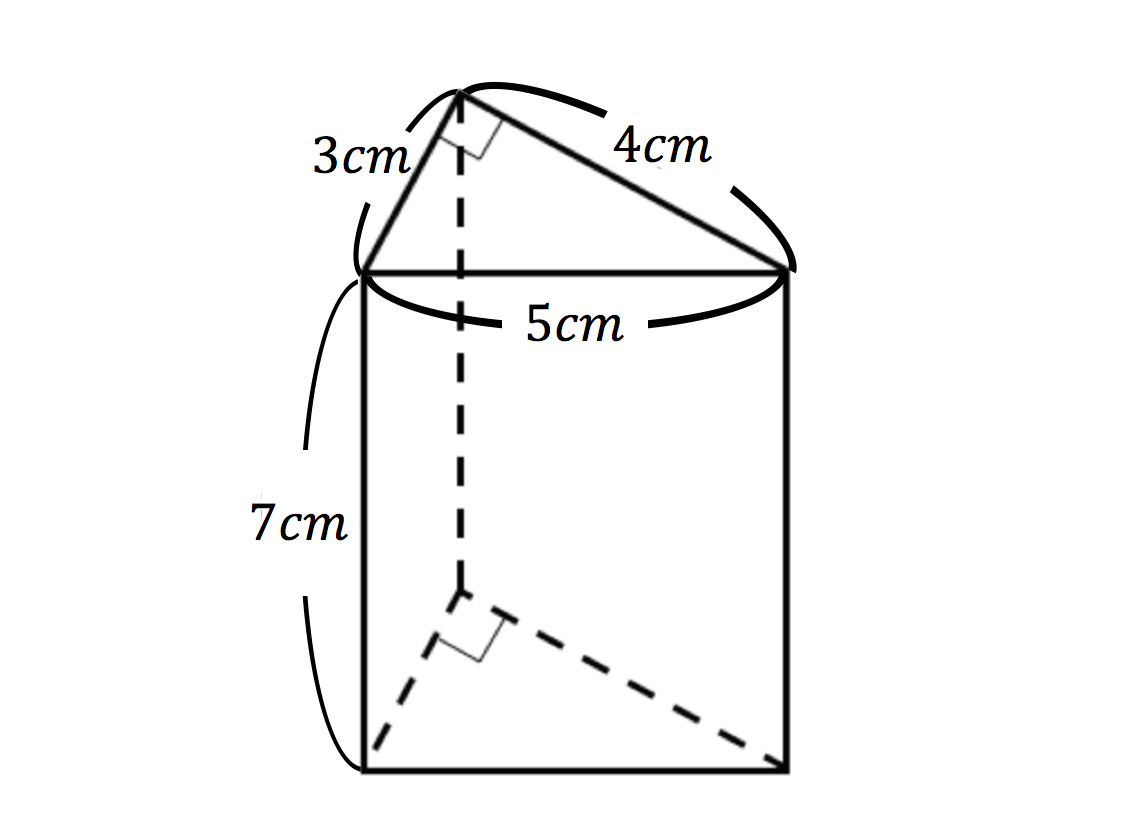
· (三角柱の体積)=(底面の三角形の面積)×(三角柱の高さ) でしたね。 この公式に当てはめていきます。 (体積)\(=(\displaystyle \frac{ 1 }{ 2 }×3×4)×7=\style{ colorred;正三角柱の底辺と高さから体積と表面積を計算します。 正三角形の一辺 a 高さ h 6桁10桁14桁18桁22桁26桁30桁34桁38桁42桁46桁50桁 体積 V 表面積 S \(\normalsize Equilateral\ triangular\ prism\\ (1)\ volume\hspace{50px} V={\large\frac{\sqrt{3}}{4}}a^2 h \\ · 円柱の体積を求めるには、与えられた半径や高さをこの公式に代入すればよいのです。 上の基本問題をこの公式を使って求める (1) r=5、h=10 だから、V=π ×5 2 ×10=250π cm 3 (2) r=4、 h=5 だから、V=π×4 2 ×5=80π cm 3 「これを覚えれば楽ちん」って思うお子さんもいるかもしれません。 しかし、これだけでは、三角柱や四角柱などの他の柱体の体積を求めるときに
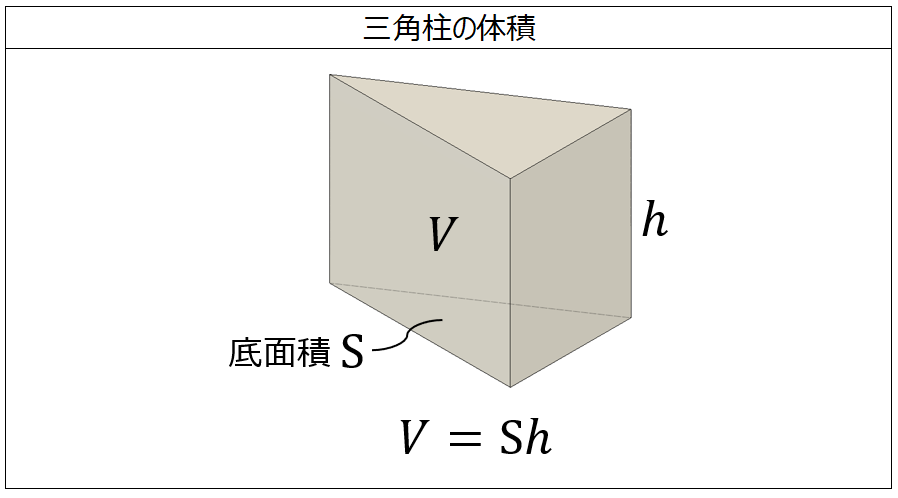
三角柱や四角柱などの体積は、底面積 $S$、高さ $h$ として、次の式で求められます。 角柱 (かくちゅう) の体積 \begin{align*} V = Sh \end{align*} 体積 = 底面積 × 高さ · 三角柱 / 円柱 の体積を求める公式 三角柱と円柱の体積を求める公式は、底面積 × 高さ です。ここでも、単位に注目してましょう。表面積の単位は cm 2 です。そして、高さの単位は cm です。cm 2 = cm × cm のことです。 · この公式を例題に当てはめると、次のようになります。 \begin{eqnarray}\frac{3×3}{2}×\frac{548}{3} = \frac{51}{2}cm^3 \\ \end{eqnarray} 切頭円柱の場合は、同じ立体を重ねて半分にするという発想で公式を証明することができましたが、三角柱の場合は一筋縄ではいきません。よって、ここでは証明を省略
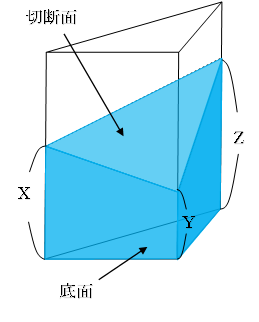
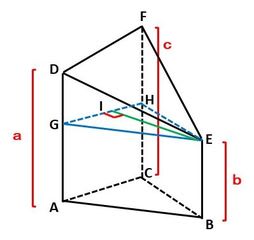
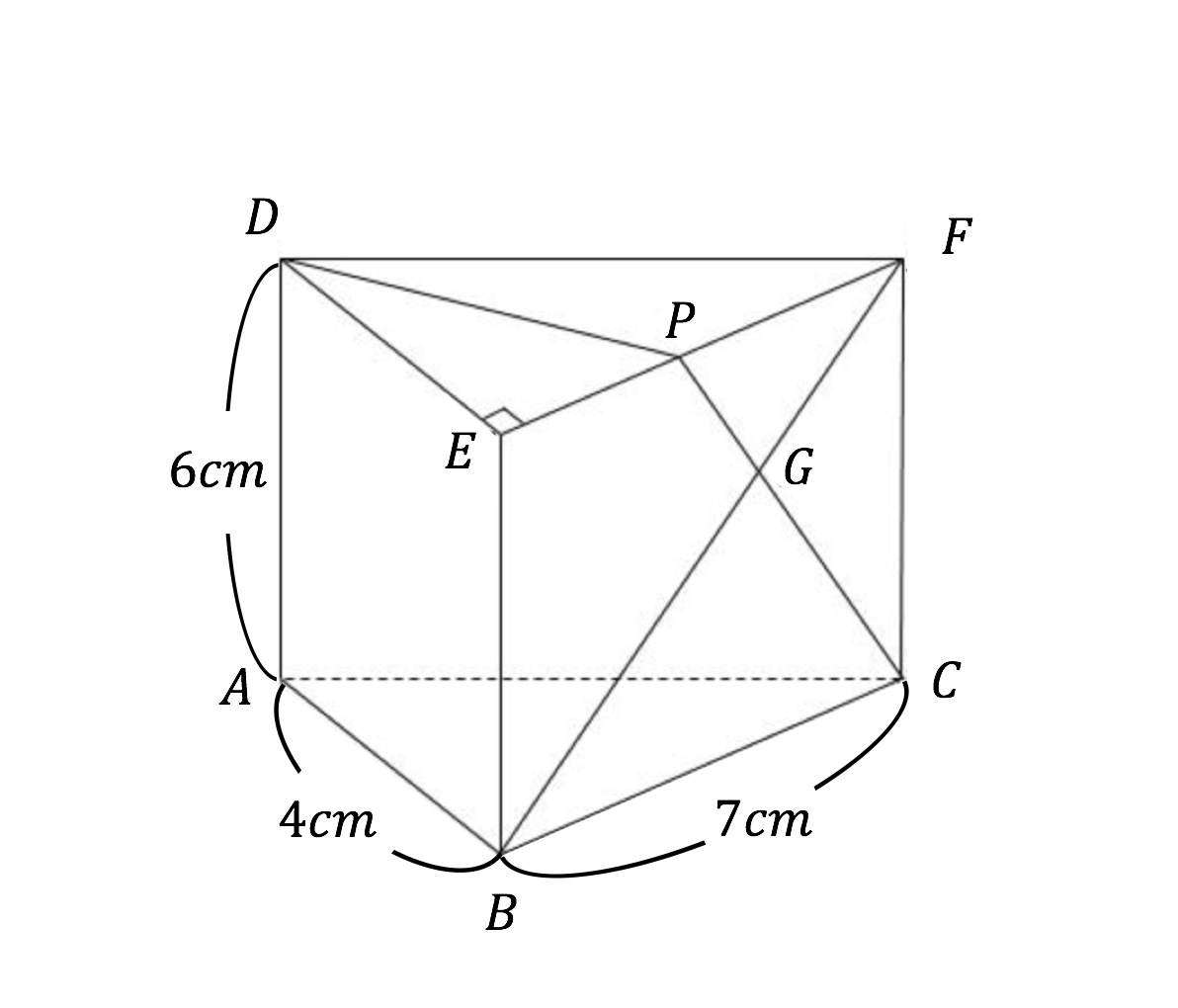
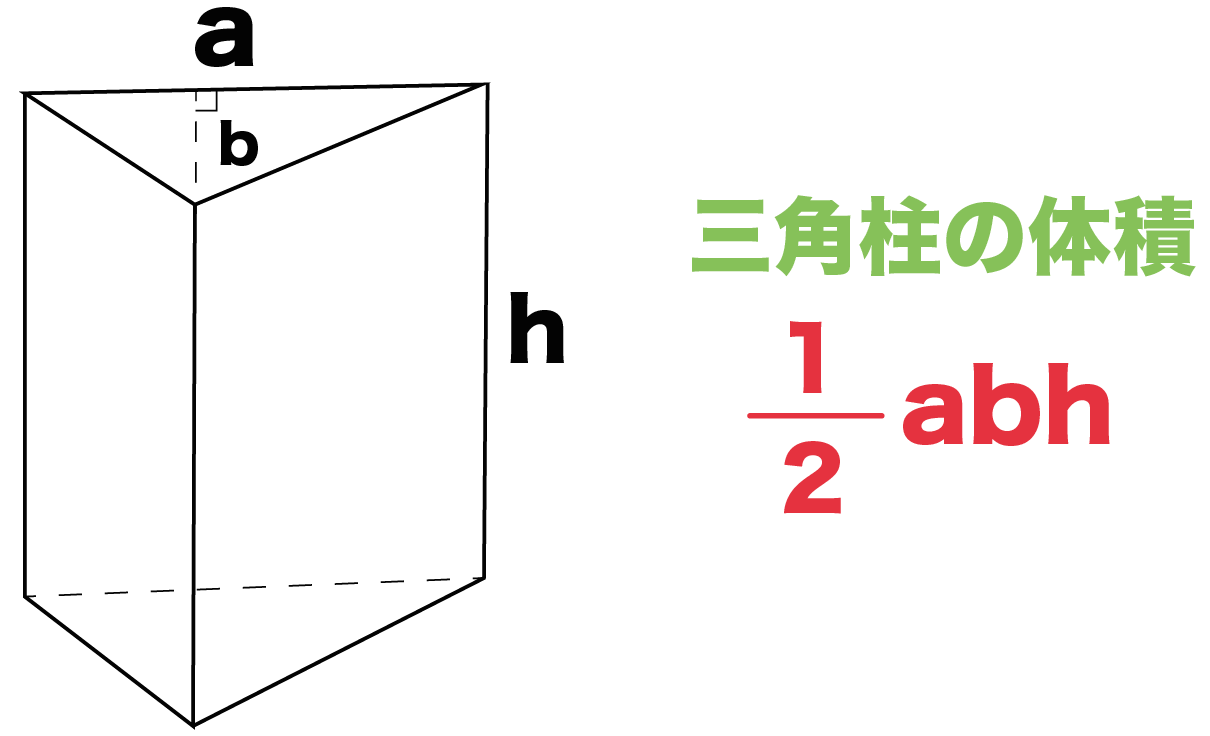
· 三角柱の体積の求め方には公式があるんだ。 三角形の底辺の長さをa、底辺からの高さをb、立体の高さがhっていう三角柱を想像してみて。 このとき、 三角柱の体積は、 1/2 abh で求めることができるんだ。 つまり、三角柱の体積を求める公式は、< 底面積×高さの平均 > と知られていますが、なぜそのようになるのか、 切断三角柱の体積の求め方を下図を用いて説明しなさい。三角柱の体積を、公式を用いて求めることができること。 三角柱の体積は、底面積×高さにまとめられることを理解すること。 三角柱の体積の求め方を利用して、他の角柱の体積も「底面積×高さ」で求められることを一般化しようとすること。 中学校の1年生では、小学校で「柱体の体積=底
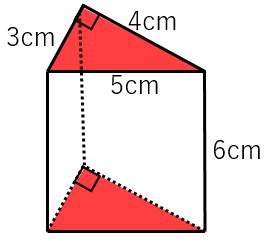



三角柱の底面積 側面積 表面積の求め方 具体例で学ぶ数学




三角柱の底面積 側面積 表面積の求め方 具体例で学ぶ数学
公式を用意する 公式はV(体積) = 1/2 x l(長さ) x w(幅) x h(高さ)となります 。 V = 底面の面積 x 高さが基本となっています。底面が三角形であれば、底面の長さ(三角形の底辺)と幅(三角形の高さ)を掛け、さらに2で割ることで面積が求められます。 · 三角柱の体積の公式 底面の三角形の面積が \(S\)、高さが \(h\) の三角柱の体積 \(V\) は、次の式で求められる。 \begin{align}\color{red}{V = Sh}\end{align}三角柱の体積 三角柱とは下図に示す図形です。 よって、 三角柱の体積=3×4÷2×5=30cm 3 です。 三角柱の体積は?1分でわかる公式、計算、表面積の求め方 四角錐の体積




体積の求め方 計算公式一覧



三角錐の体積の公式は 1分でわかる公式 問題 底面積との関係
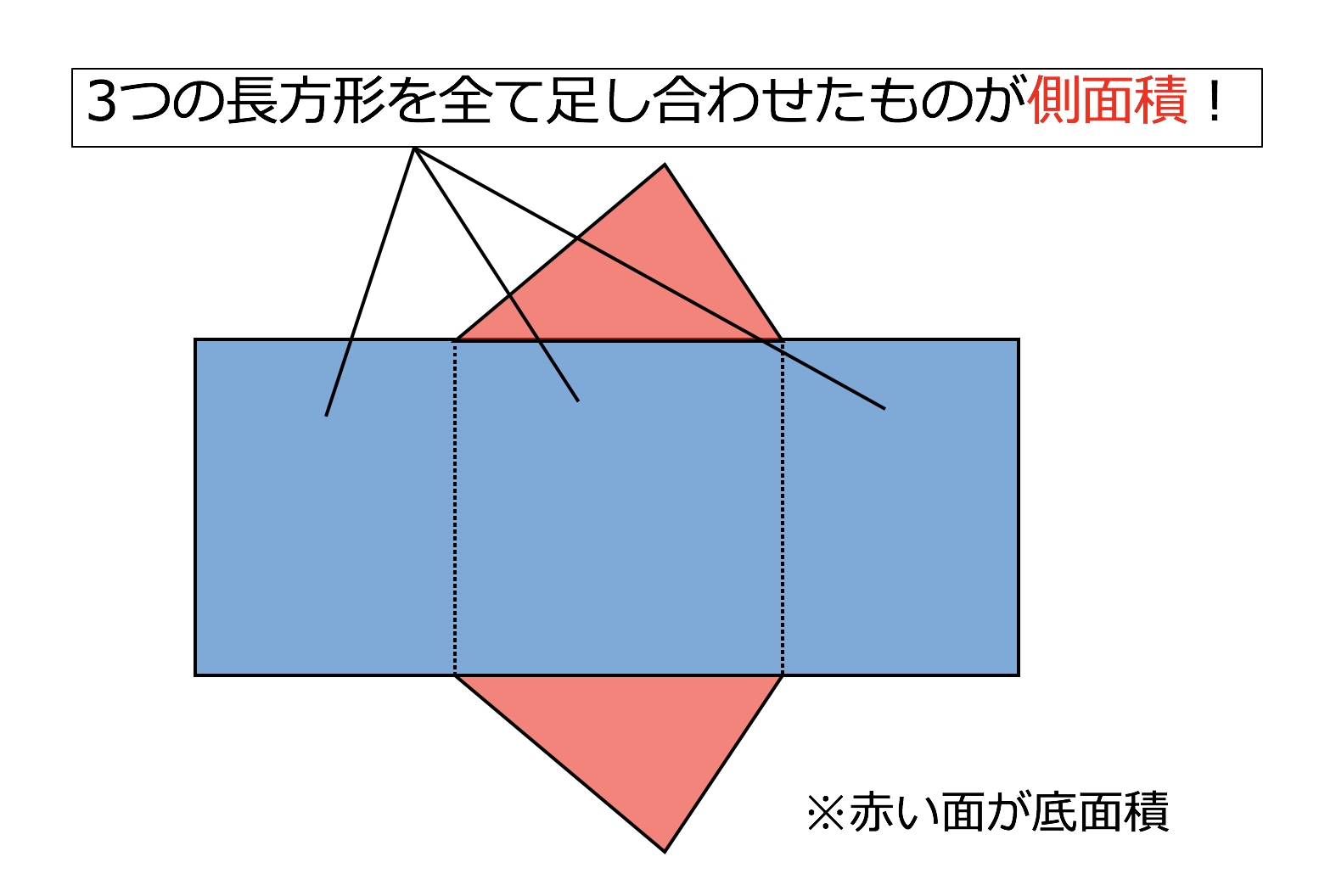
· 続いて、三角柱の表面積の公式は「底面積 × 2 側面積」でしたね。 すると、底面積は先に求めた$8cm^2$ですね。 側面積の求め方ですが 「高さ × 底面の周の長さ」で求めることができテーマ: 立体図形 昨日の21渋谷幕張一次の最後の大問5にインスパイアされて、断頭三角柱の体積の公式って、なんで高さ平均を求めるんでいいんだっけ? ってのが気になった。 ⬇︎の問題でジーニアスの教誓先生が公式の意味を分かりやすく説明して角柱の体積の公式=底面積×高さ この公式は、中学校でもよく使うので、声を出して覚える練習すると中学の体積の勉強がわかりやすくなります。 練習問題 次の立体の体積を求めましょう 問題① 底面の形は五角形です 底面を3つの三角形にわけて面積を求めます 合計すると 15+25+12=52



三角柱の体積の求め方 回転体の側面積の考え方 中学1年数学 空間図形
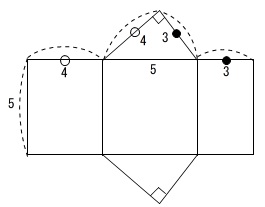



表面積や体積の求め方 三角柱 四角柱 円柱 球や半球
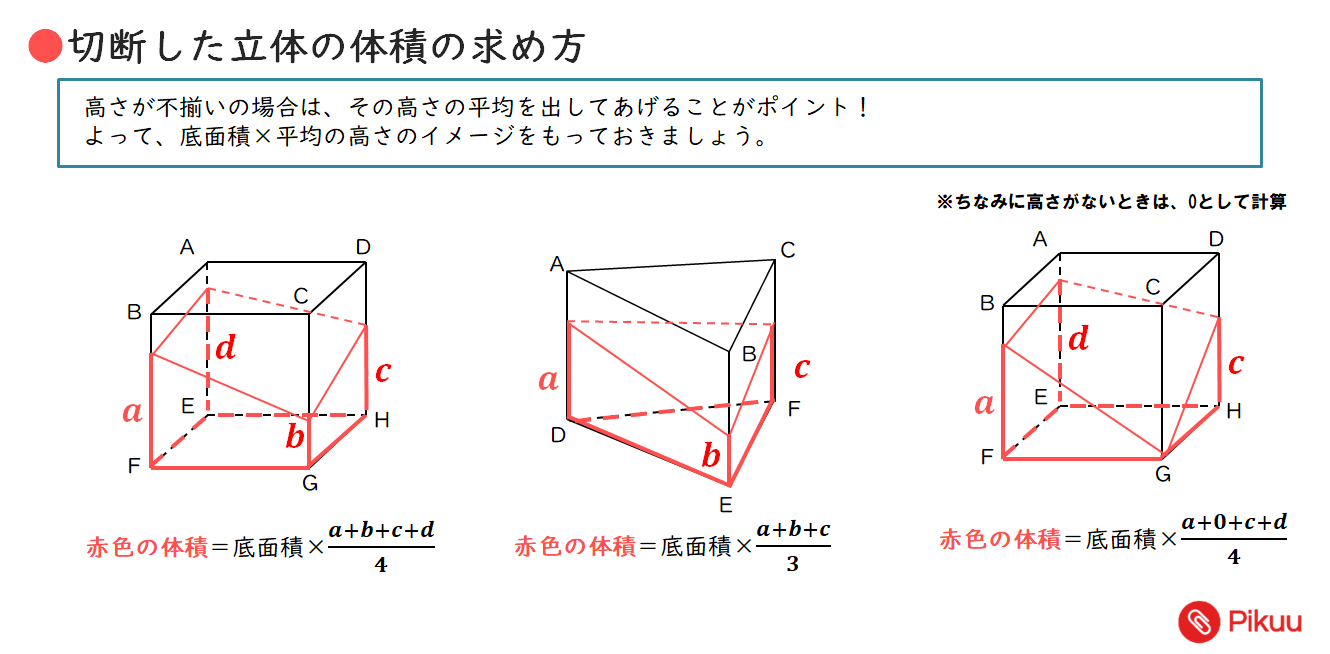
角柱と角錐の体積を求める公式 角柱と角錐の体積を求めるための公式があります。 角柱の体積=底面積×高さ 角錐の体積=底面積×高さ×1/3 これは円柱や円錐のときも同じで、円柱の体積は、「底面の円の面積×高さ」、円錐の体積は、「底面の円の面積×高/10/16 · 1:高校受験数学の問題で、四角柱の頭部を切断した残り部分の体積を求める公式として 底面積x (abcd)/4(abcdはそれぞれ底面に垂直な辺の長さ) つまり、体積=底面積☓底面に垂直な辺の長さの平均 があるそうですが、なぜそうなるのですか? 同じ立体解説 角柱,円柱の体積 底面積が ,高さが の円柱や角柱(三角柱,四角柱,五角柱,・・)の体積 は, (底面積×高さ) で表わされます。 特に円柱では,底面の半径をrとすると だから になります。



1



1
三角柱の体積は,角柱の体積の公式を使って求 めることができる。 底面の形が直角三角形なので,三角形の面積の 公式を使って底面積を求めると, 角柱の体積の公式は,底面積×高さなので, となり,三角柱の体積は42㎤になる。 角柱の体積=底面積×高さ6年算数 立体の体積 その1 子どもの学習支援 by いっちに算数 スマホ版 立方体 直方体 6年生は、上の図のように5年生で勉強した「直方体や立方体」の体積の求め方を生かして、下の図のような「三角柱などの角柱や円柱」の体積の求め方を勉強します。だから三角柱の体積=底面積×高さになる。'' この展開には注意が必要なので述べておきます。 ①三角柱を底面が特別な三角形(直角三角形)のみ扱って、三角柱の公式を一般化してしまいがちです。 一般の三角形も扱う必要があります。 ②この式変形が子どもたちにはなかなか納得できない




角柱 円柱の表面積と体積の公式 数学fun
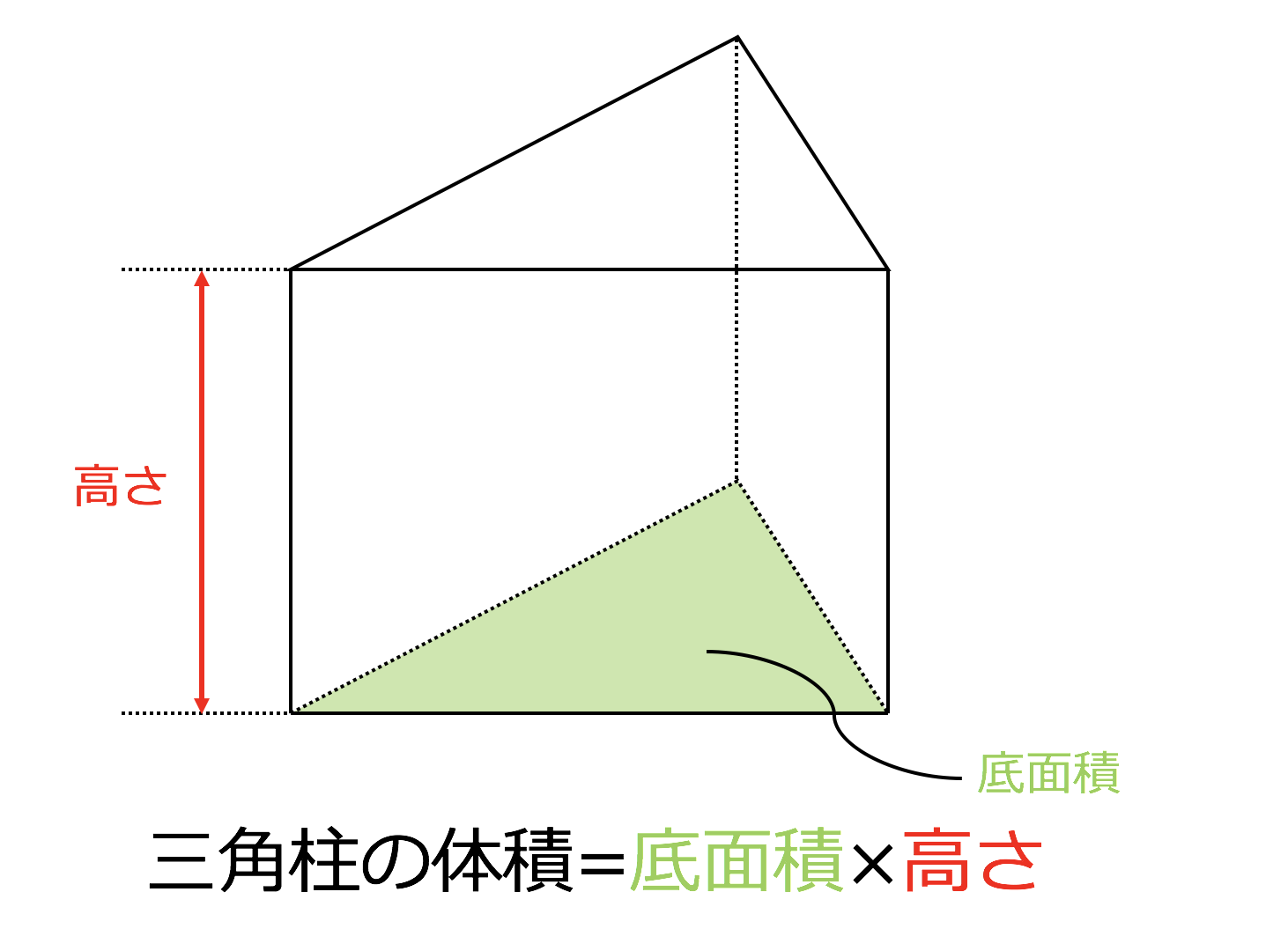



3分で分かる 三角柱の体積 表面積の公式 表面積 をわかりやすく 合格サプリ
正四面体の体積から辺の長さと表面積を計算します。 正三角柱の体積 正三角柱の体積 正三角柱の底辺と高さから体積と表面積を計算します。 正三角柱の高さ 正三角柱の高さ 正三角柱の体積と底辺から高さを計算します。 正四角柱の体積 正四角柱の体積他図形の体積、三角柱の体積など下記も勉強しましょう。 台形の面積を求める公式 台形の面積を求めるときには、次の公式を使います。 このとき、辺ap、辺dc、辺rqを延長すると、三角錐oadrになります。 考えるのが良くないと言っているのではありませんが、考えてもろくなものは出てきませあとまあくクラブ 算数・数学 公式一覧 面積の公式 平行四辺形の面積 底辺 × 高さ 三角形の面積 底辺 × 高さ ÷ 2 台形の面積 (上底+下底)×(高さ)÷ 2 ひし形の面積 対角線 × 対角線 ÷ 2 円の公式 円の面積 半径×半径×3.14 円周 直径×3.14 体積の公式




中学数学 三角柱の体積の求め方と公式 5秒でわかる なぜか分かる はかせちゃんの怪しい研究室



3分で分かる 三角柱の体積 表面積の公式 表面積 をわかりやすく 合格サプリ
· 三角柱の体積は、次の公式で求められます。 三角柱の体積=底面積×高さ 三角柱の底面積は三角形の面積なので、三角形の面積×高さで求めることができます。四角柱,三角柱,円柱の体積 V は,底面積 S と高さ h を使って表すことができます. V=Sh 特に,円柱については,底面の半径が r であるとき,底面積が S=πr 2 と書けるから V=πr 2 h と書くこともできます. ※簡単なことのように見えますが,底面と高さとが直角になっている場合だけこの公式がこれは「断頭三角柱」と呼ばれるものですね。 (頭とお尻を切断したので断頭断尻三角柱と言いたいかもしれませんが) ところでこの立体、どこかで見たことありませんか? そう、問題に出した「四角すい」ですよね! つまり、



三角柱の表面積 底面積も と体積を求める公式と計算問題 単位との関係 ウルトラフリーダム



トップ100三角柱 の 体積 公式 最高のぬりえ
台形の面積=(a+b+4(a+b)/2)/6×h=(a+b)/2×h 半球の体積=(πr2+3/4πr2×4)/6×r=2/3πr3 S:本当だ。 すごい。 T:さて、この公式を使うと、 三角形の面積の場合は、b=0で、c=a/2だから、 S=(a+4a/2)/6×h=(1/2)・ah 錐体の体積の場合は、b=0で、c=a/4 (2乗に比例する)だから、 V=(a+4a/4)/6×h=(1/3)・ah · 三角形の角の二等分線の性質・定理の証明がわかる5ステップ 中1数学 1554 計算公式三角柱の体積の求め方がわかる2つのステップ 中3数学 計算公式立方体の対角線の長さの求め方がわかる3ステップ 中1数学




簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




計算公式 三角柱の体積の求め方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく




三角錐 四面体 の体積の公式 Schoolmath S Diary




3分で分かる 三角柱の体積 表面積の公式 表面積 をわかりやすく 合格サプリ




体積の求め方ー四角柱ー 小学生 算数のノート Clear



また来てね問題集 図形問題 解答と解説 中学受験 家庭教師 東京の算数家庭教師さんじゅつまん



三角柱の体積は 1分でわかる公式 計算 表面積の求め方



三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学



小学算数 立体と体積 直方体 立方体 三角柱 円柱 四角すい 円すい 辺 面 頂点 展開図 体積と表面積の公式 学習ポスター クイズテスト やってみよう ちびむすドリル 小学生学習ポスター テスト 家庭学習シート 3ステップ学習



切断された三角柱 切断三角柱 の体積の求め方 まいにち一題 中学受験過去問題研究




計算公式 三角柱の体積の求め方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく




三角柱の体積 表面積の求め方が図で誰でも即わかる 展開図も紹介 高校生向け受験応援メディア 受験のミカタ




多くの教師が失敗する角柱の体積の求め方 算数を究める




三角柱の体積 四角柱の体積の1 2 算数嫌い0 ゼロ 先生のブログ




三角柱の体積の求め方 公式 小学生 中学生の勉強
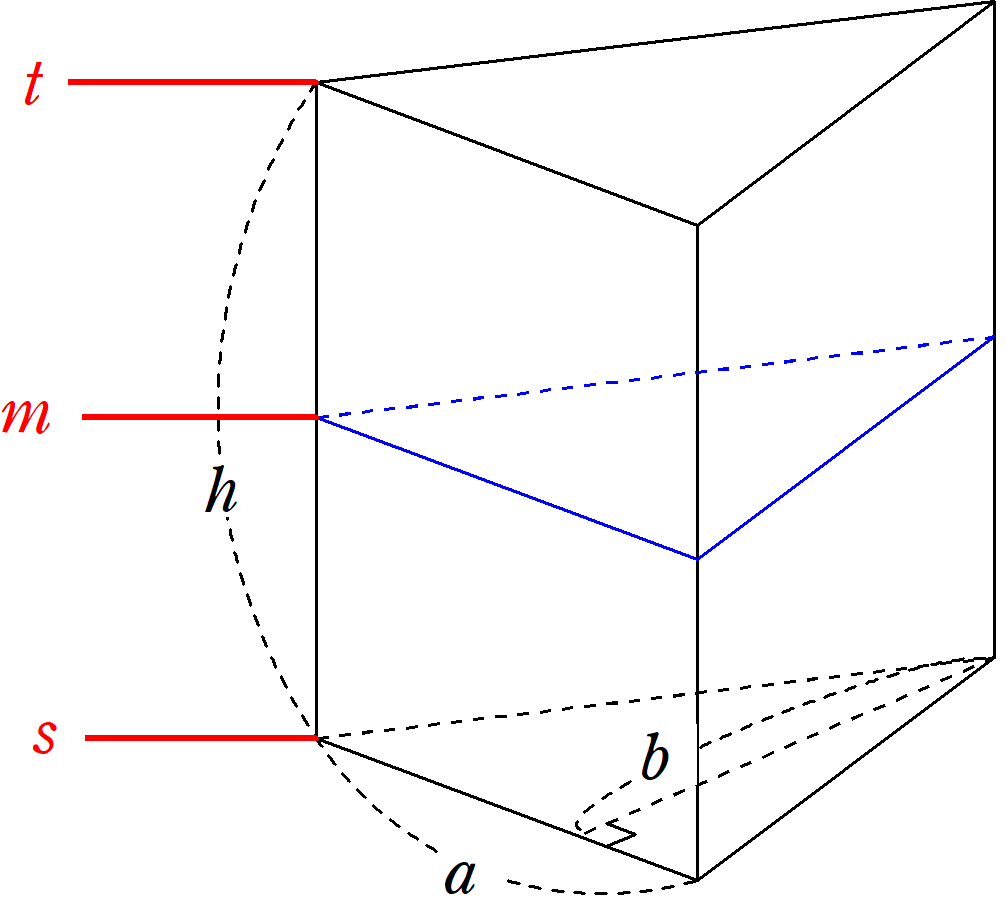



シンプソンの公式 応用編 Fukusukeの数学めも



Mathematics 立体の切断 高校入試に出る難しい問題 働きアリ




計算公式 三角柱の体積の求め方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく
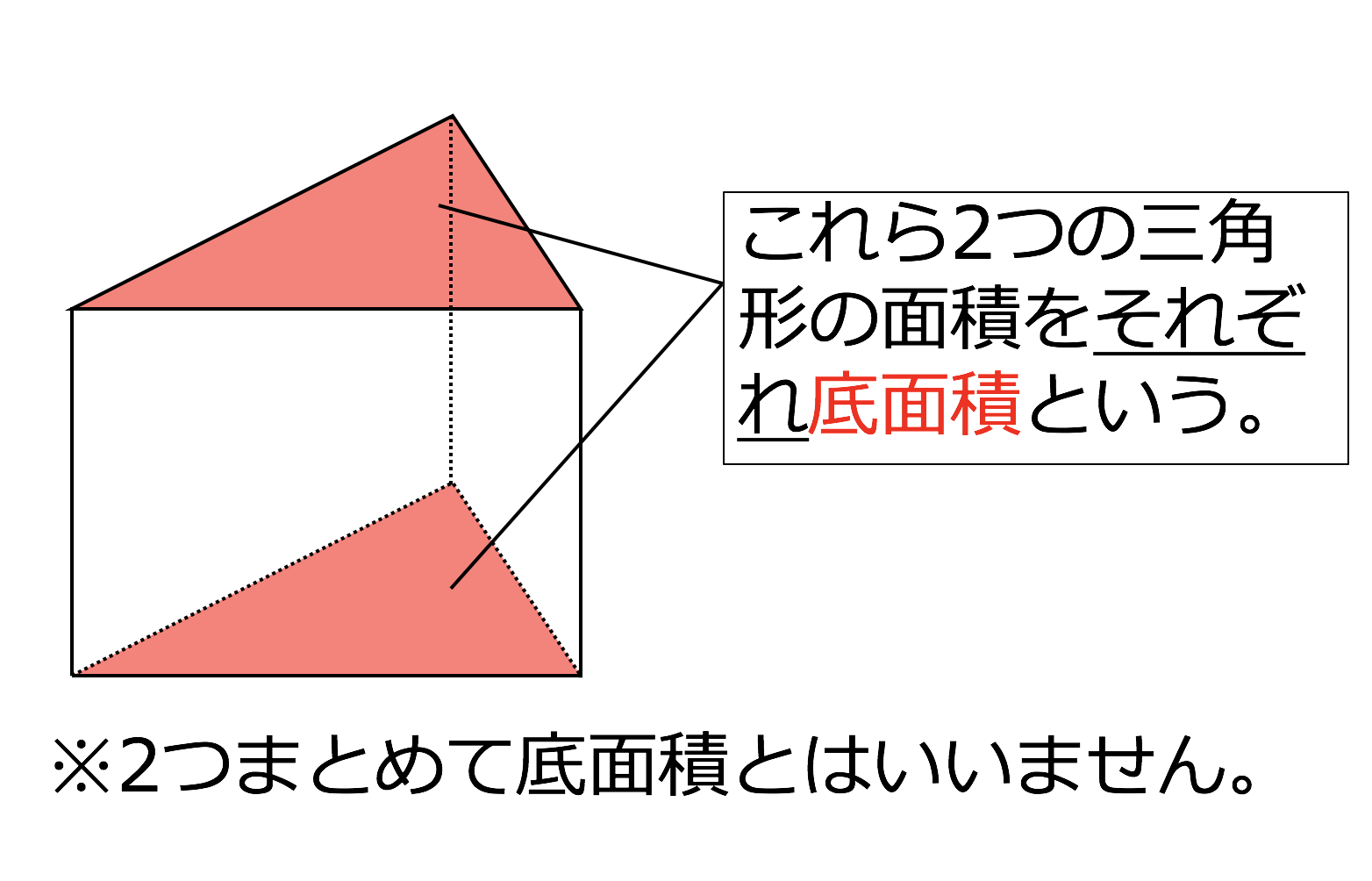



3分で分かる 三角柱の体積 表面積の公式 表面積 をわかりやすく 合格サプリ
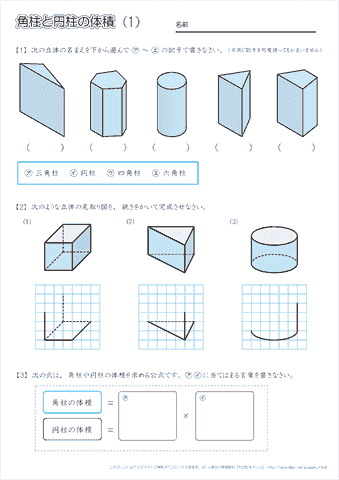



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生



四角柱の体積の公式は 1分でわかる求め方 公式と計算 表面積




空間図形15 断頭三角柱の体積 Youtube




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット



2つの三角柱が重なった体積問題 14年 早稲田中学校 恋する中高一貫校 適性検査 徹底攻略




体積の求め方 計算公式一覧




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学




小学算数 立体と体積 直方体 立方体 三角柱 円柱 四角すい 円すい 辺 面 頂点 展開図 体積と表面積の公式 学習ポスター クイズテスト やってみよう ちびむすマンスリー 学習ポスター テストクイズ 3ステップ学習 算数 小学校 算数 学習



三角錐の体積の公式は 1分でわかる公式 問題 底面積との関係



切断された三角柱 切断三角柱 の体積の求め方 まいにち一題 中学受験過去問題研究




三角柱の体積 表面積の求め方が図で誰でも即わかる 展開図も紹介 高校生向け受験応援メディア 受験のミカタ




計算公式 三角柱の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




空間図形15 断頭三角柱の体積 Youtube




三角柱の体積 表面積の求め方が図で誰でも即わかる 展開図も紹介 高校生向け受験応援メディア 受験のミカタ



1




三角柱の投影図の体積の求め方を教えてください Clear




現役プロ講師が教える 断頭三角柱の体積公式 高校入試数学で覚えておくとよい公式集 Youtube
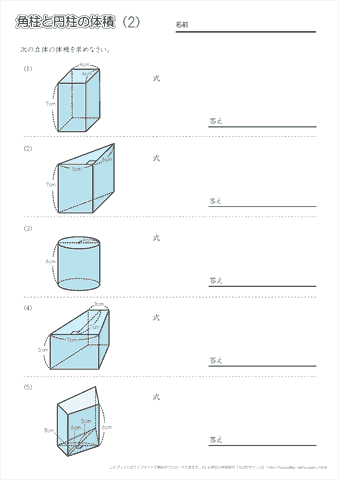



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生




三角柱の体積 表面積の求め方が図で誰でも即わかる 展開図も紹介 高校生向け受験応援メディア 受験のミカタ




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




計算公式 三角柱の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
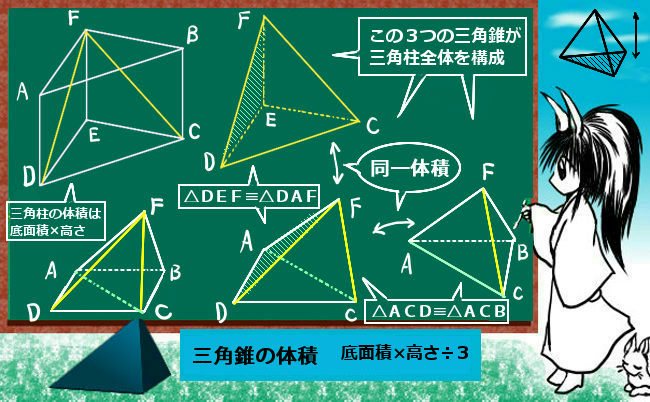



立体の体積 理数系無料オンライン学習 Kori




体積の求め方 計算公式一覧



切断された三角柱 切断三角柱 の体積の求め方 まいにち一題 中学受験過去問題研究
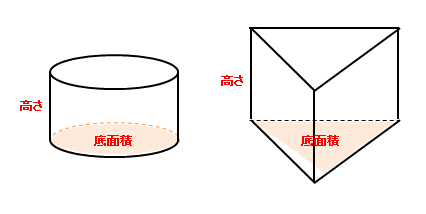



小学算数 立体の体積の公式と単位 立方体 直方体 円柱 三角柱 偏差値40プログラマー




三角柱の体積の求め方 公式 小学生 中学生の勉強




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学



Math ややこしい立体の体積は 柱と錐に分割して求める 働きアリ
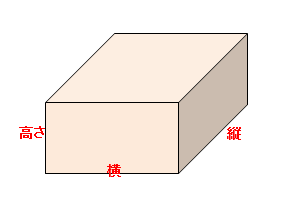



小学算数 立体の体積の公式と単位 立方体 直方体 円柱 三角柱 偏差値40プログラマー




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット
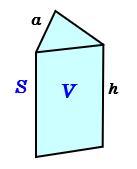



正三角柱の体積 高精度計算サイト



三角柱とは 体積 表面積の公式や求め方 計算問題 受験辞典




公式一覧 立体の体積 表面積の求め方 円柱 三角柱 円錐 三角錐 球




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



Math ややこしい立体の体積は 柱と錐に分割して求める 働きアリ The 2nd
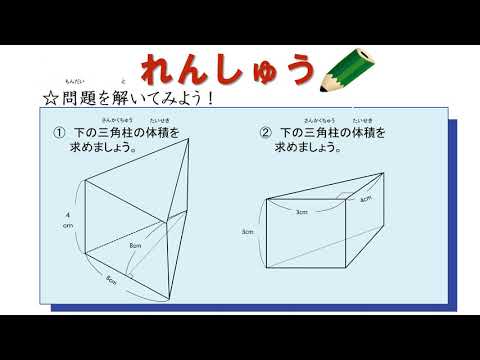



小6 角柱と円柱の体積 三角柱の体積 日本語版 Youtube




多くの教師が失敗する角柱の体積の求め方 算数を究める



三角柱の体積の公式教えてください 底面積 高さだよ 底面は三角 Yahoo 知恵袋




6年算数立体の体積1 教え方




体積の求め方 計算公式一覧



Http Www Nc Gunma Boe Gsn Ed Jp Action Common Download Main Upload Id 3439




角柱の体積の公式 求め方は底面積と高さに注目するだけだ 中学や高校の数学の計算問題




断頭三角柱の公式と証明 Youtube




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun



小6算数 角柱と円柱の体積 指導アイデア みんなの教育技術



三角柱の体積を求める時にテキストでは2分の1と出ているんですがこれは何なんで Yahoo 知恵袋



三角柱の体積の公式を教えて下さいm M ついでにこの計 Yahoo 知恵袋



切断三角柱の体積の求め方 東久留米 学習塾 塾長ブログ




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト



体積の計算 三角柱 製品設計知識




三角柱の体積の求め方 公式 小学生 中学生の勉強



体積の公式は 1分でわかる求め方と覚え方 一覧 三角柱 円柱 三角錐の体積




小6 算数 小6 26 角柱と円柱の体積 基本編 Youtube




三角柱の体積を求める問題です 三平方 ピタゴラスの定理の応用です 解ける方解き方 Clear



Math ややこしい立体の体積は 柱と錐に分割して求める 働きアリ



3分で分かる 三角柱の体積 表面積の公式 表面積 をわかりやすく 合格サプリ



三角柱の体積は 1分でわかる公式 計算 表面積の求め方




3分で分かる 三角柱の体積 表面積の公式 表面積 をわかりやすく 合格サプリ




ボード 勉強法 のピン



計算公式 三角柱の体積の求め方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく



三角柱の体積は 1分でわかる公式 計算 表面積の求め方



3分で分かる 三角柱の体積 表面積の公式 表面積 をわかりやすく 合格サプリ




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット




3分でなるほど 三角柱の体積 表面積の求め方をマスターしよう 数スタ




角錐 円錐の体積と表面積の公式 数学fun



高校入試対策数学 切断した立体の体積を求める練習問題 Pikuu




二側錐三角柱 Biaugmented Triangular Prism Japaneseclass Jp




三角柱の体積の求め方 公式 小学生 中学生の勉強




三角柱の体積の求め方 小学生向けに問題使って解説するぞ 中学数学 理科の学習まとめサイト




三角柱の体積の求め方 公式 小学生 中学生の勉強



3



0 件のコメント:
コメントを投稿